Vamos a recordar y
precisar, el significado de una serie de términos y expresiones necesarios para
la comprensión del presente Capítulo.
Si sobre un cuerpo actúa una fuerza F, dando lugar a una aceleración a, entonces su masa m es:
Figura 1
Figura 2
En muchos casos el módulo
de elasticidad es constante durante la zona elástica del material, indicando un
comportamiento lineal del mismo (ley de Hooke).
El módulo de elasticidad indica la rigidez de un material: cuanto más rígido es un material mayor es su módulo de elasticidad.
En el caso unidimensional, si una fuerza F sobre un sistema produce una deformación del mismo u, la rigidez del sistema es:
la Fig. 1.,
una carga de 40 Tm en el extremo libre.
Esta carga o fuerza, causa un esfuerzo en la sección de 40.000 Kg/125 x 60 = 40.000 Kg/7.500 mm2 =5,33 Kg .
/mm2. En este caso, por estar el acero dentro de su límite elástico,
se extenderá en dirección proporcional al esfuerzo. Los aceros dulces en
Construcción Naval tienen un límite elástico de 25 Kg/mm2; en la
práctica ' se procura, por seguridad, que los esfuerzos por tracción no sean
superiores a 10 Kglmm2. En los Aceros de Alta Resistencia a la Tracción , usados
actualmente en algunas zonas de ciertos buques, su límite elástico está
comprendido entre 33 y 45 Kg/mm2; sin embargo, por seguridad, se
procura que la tracción en los elementos estructurales no pase de 15 Kg/mm2.
Figura 3 Barra de acero prismática sometida a esfuerzos por tracción.
Figura 4
La curva obtenida tiene los siguientes puntos característicos:
Masa
La masa de un cuerpo se
define como su oposición a ser acelerado. Si sobre un cuerpo actúa una fuerza F, dando lugar a una aceleración a, entonces su masa m es:
m = F/a
de acuerdo con la Segunda Ley de Newton.
A partir de la
expresión anterior, se deduce que también se puede definir la masa de un cuerpo
como el cociente entre la fuerza con la que la tierra atrae dicho cuerpo y la
aceleración de la gravedad.
Fuerza
Se denomina fuerza a cada
una de las acciones mecánicas que se producen entre los cuerpos. Una fuerza se
caracteriza por:- Su punto de aplicación sobre el cuerpo
- Su dirección o línea de acción
- Su sentido, que puede ser en cualquiera de
los dos opuestos que define la línea de acción
- Su magnitud que indica la intensidad de la
misma.
Las fuerzas que pueden
actuar sobre un cuerpo se clasifican en fuerzas de volumen y fuerzas de
superficie.
Las fuerzas que se
ejercen entre dos cuerpos son siempre iguales y de sentidos opuestos de acuerdo
con la 3ª Ley de Newton.
Carga. Es el término general que se lisa para indicar la fuerza o peso que actúa
sobre un cuerpo, sometiendo la estructura de éste a una condición de esfuerza,
que tiende a producir cambios de forma en el mismo. Se usa como unidad
Toneladas x metro.
Esfuerzo. Es el efecto de la carga sobre el cuerpo, o sea, la carga de trabajo de
su estructura. Equivale a la medida de resistencia de un material, a las
fuerzas que tienden a producir su deformación. Se expresa en Kg/mm2.
Deformación. Es el efecto del esfuerzo, y es la medida de la alteración de las formas.
Se expresa en tanto por ciento del largo original. ,
Módulo de elasticidad o de Young. El módulo de elasticidad (E), también llamado
módulo de Young, es un parámetro característico de cada material que
indica la relación existente (en la zona de comportamiento elástico de dicho
material) entre los incrementos de tensión aplicados (dσ) en el ensayo de
tracción y los incrementos de deformación relativa (dε) producidos.
E = dσ/dε
Equivale a la tangente en
cada punto de la zona elástica en la gráfica tensión-deformación (σ – ε)
obtenida del ensayo de tracción. (Fig. 2).
El módulo de elasticidad indica la rigidez de un material: cuanto más rígido es un material mayor es su módulo de elasticidad.
Rigidez
La rigidez de un sistema
mecánico se define como su oposición a ser deformado. En el caso unidimensional, si una fuerza F sobre un sistema produce una deformación del mismo u, la rigidez del sistema es:
K = F/u
Por ejemplo, un resorte o
muelle de rigidez k se deforma u cuando se le
aplica una fuerza F.
La rigidez de un sistema
no es necesariamente constante con su deformación, por lo que resulta más
apropiado definir la rigidez en cada instante como la derivada de la fuerza
respecto a la deformación:
K = dF/du
En general, en el caso
tridimensional, es posible definir una matriz de rigidez de un sistema (matriz
[k] de tamaño 6 x 6) que relaciona las fuerzas y momentos en las tres
direcciones del espacio con las deformaciones lineales y angulares en las tres
direcciones.
Tensión o Tracción. La resistencia que un material ofrece a que lo,
estiren.
A la barra de acero de la
(Fig. 3), firme a la superficie A por el extremo P, le aplicamos según el
vector de Esta carga o fuerza, causa un esfuerzo en la sección de 40.000 Kg/125 x 60 = 40.000 Kg/7.500 mm2 =
Figura 3 Barra de acero prismática sometida a esfuerzos por tracción.
Ensayo de tracción
El ensayo de tracción es
un ensayo en el que se somete a tracción a una probeta normalizada de un
material hasta que se alcanza la rotura.
La probeta suele ser
cilíndrica con ensanchamientos en sus extremos para su fijación a las mordazas
de la máquina.
La máquina empleada para
el ensayo de tracción es una máquina universal de ensayos que aplica un
esfuerzo sobre la probeta para alargarla y mide el alargamiento producido y el
esfuerzo aplicado. A partir de dichas medidas de fuerza y alargamiento y de las
dimensiones de la probeta (sección y longitud inicial) se obtiene una gráfica
durante el ensayo que representa la tensión s (Fuerza aplicada / sección
de la probeta) frente a la deformación relativa de la probeta e
(alargamiento / longitud inicial).
En la figura se muestran
ejemplos de dos curvas correspondientes al ensayo de tracción de un material
frágil y uno dúctil.
La curva obtenida tiene los siguientes puntos característicos:
-
Y:
Límite de fluencia (punto que marca el fin de la zona de comportamiento
elástico, en el que la deformación permanente alcanza el 0.2 %)
-
U:
Límite de resistencia última (máxima tensión que resiste el material antes de
romper)
- F: Límite de rotura (punto en el que rompe el material)
Video Ensayo de Tracción:
Ductilidad
La ductilidad es la
capacidad de un material para sufrir deformaciones sin romperse. Es la
propiedad opuesta a la fragilidad.
Por convención se
consideran dúctiles aquellos materiales que, en el ensayo de tracción, admiten
alargamientos relativos superiores al 5 % antes de la rotura.
Algunos ejemplos de
materiales dúctiles son el acero o el aluminio.
Fragilidad
La fragilidad es la
incapacidad de un material para sufrir deformaciones importantes sin llegar a
romper. Es la propiedad opuesta a la ductilidad.
Por convención se
consideran frágiles aquellos materiales que, en el ensayo de tracción, llegan a
romper antes de que se alcance un alargamiento relativo del 5 %.
Algunos ejemplos de
materiales frágiles son el hormigón o el vidrio.
Compresión. La resistencia que un material ofrece a las fuerzas o cargas que lo
comprimen, se llama Resistencia a la Compresión. En general, se supone que el acero
dulce, tiene la misma resistencia a la tracción que a la compresión; pero
normalmente la compresión está relacionada con la flexión, y reforzada
localmente por el pandeo. Como vimos en el esquema general de los esfuerzos del
casco, había una situación, que es la de «Arrufo»,
que la cubierta se comprime (localmente según la zona, más o menos); este
fenómeno es aumentado porque los refuerzos transversales del casco, están
separados por una «clara» (separación
entre cuadernas de construcción), entre estos esfuerzos hay efectos de pandeo
en la cubierta por la compresión general; y todavía más, por un aumento
circunstancial de peso en la zona, por embarque de agua (peso y energía
cinética) que acentúa el esfuerzo deformante por pandeo.
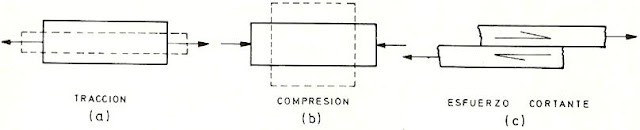
En la (Fig. 4, a, b),
deformación dentro del límite elástico por tracción y compresión.
Esfuerzo cortante. El efecto de dos fuerzas actuando en sentido
paralelo y direcciones opuestas. En la (Fig. 4, c) tiende a que una pieza se
deslice sobre la otra. Cuando los barcos se remachaban, era el principal
esfuerzo que aguantaba la caña del remache, ayudado por la compresión que
ejercían las cabezas, para evitar el deslizamiento. Ya veremos la importancia
de estos esfuerzos en el casco del buque, por fuerzas verticales de dirección
opuesta, consideradas en cada sección.
Figura 4 (a), (b) y (c) Deformaciones por tracción y compresión.
Las fuerzas aplicadas a un elemento estructural pueden inducir un efecto de deslizamiento de una parte del mismo con respecto a otra. En este caso, sobre el área de deslizamiento se produce un esfuerzo cortante, o tangencial, o de cizalla (fig. 4 d). Análogamente a lo que sucede con el esfuerzo normal, el esfuerzo cortante se define como la relación entre la fuerza y el área a través de la cual se produce el deslizamiento, donde la fuerza es paralela al área. El esfuerzo cortante (τ) se calcula como (fig. 4 e):
Esfuerzo cortante =
fuerza / área donde se produce el deslizamiento.
τ= F / A
donde,
τ: es el
esfuerzo cortante
F: es la fuerza que
produce el esfuerzo cortante Figura 4 (d)
τ
= P/A Esfuerzo cortante
Las deformaciones debidas a los esfuerzos
cortantes, no son ni alargamientos ni acortamientos, sino deformaciones
angulares g, como se muestra en la fig. 4
f.
Figura 4 (f) Deformación debida a los esfuerzos cortantes.
Video Fuerzas Cortantes en Vigas.
También puede establecerse
t = G x g
Los módulos de elasticidad E y G están relacionados mediante la expresión (MOTT, 1999)[2]:
G = E / (2 (1 + m))
donde,
m: es la relación de Poisson[3] del material
Flexión. Una pieza experimenta esfuerzos por flexión, cuando está sometida a cargas o fuerzas que se ejercen en sentido transversal (normalmente perpendiculares a su eje longitudinal). Bajo la acción de estas cargas, la pieza se deforma; si era recta, se curva, acortándose las fibras de la parte cóncava y alargándose las de la convexa. Tiene una fibra neutra que no varía de longitud, y pasa por los centros de gravedad de la secciones de la pieza.
Vamos a ver los efectos de un peso situado en medio de
una viga, que tiene los extremos apoyados (Fig. 5, a ).
Figura 5 (a) Viga apoyada y flexionada, (b) viga cortada por rigidez y exceso de carga.
La carga producida en la viga por el peso P, se la
reparten los dos extremos apoyados, que ejercerán una fuerza en dirección
opuesta, llamada reacción de la viga. Naturalmente el peso P será igual a la suma
de las reacciones (R + R1). Este reparto de cargas, intentarán
flexionar la viga, como se ve en la (Fig. 5a) Si la viga fuera completamente
flexible, se curvaría y ya está; pero si es más o menos rígida (como sucede en
la práctica), resistirá a la deformación por flexión. Las fuerzas entonces
cortarán la viga, como en la (Fig. 5 b), o al menos lo intentarán.
Obsérvese que las mismas cargas, intentan flexionar y
cortar la viga, por lo que hay una relación entre estos dos efectos.
Se conoce con el nombre de «Esfuerzo cortante», la suma algebraica de todas las fuerzas
(cargas y reacciones), que actúan a un lado de la viga, y que serán iguales a
la del otro; pero actuando en dirección opuesta. En la (FigCortante a un lado del centro, por ejemplo, a la derecha, será (+ 3-2) = + 1 Tm
de (E C); igualmente a la izquierda (+3 -4) = -1 Tm de (EC). Los signos son
para determinar la dirección de las fuerzas. En el centro de la viga al tener
un esfuerzo cortante de 1 Tm. hacia arriba y 1 Tm. hacia abajo, ése es su
valor.
Figura 6 Esfurzo cortante a lo largo de la viga.
El efecto de la flexión que depende (Fig. 7) del peso y
donde lo situemos, viene dado por su Momento Flector, que es el producto del
peso por la distancia a la sección que estamos considerando. La viga de la Fig. Apoyada en uno de sus
extremos y cargada en el otro, nos va a servir como caso más simple, para el
cálculo del Momento flector. Si la carga es P en Tm, y la distancia a la
sección considerada (s) es (x) en metros, el Momento flector (M) en la sección
(s) = P. x (Tonelada. metro).
En la práctica no es tan fácil, porque dependen cómo
estén los pesos, concentrados o diseminados, y cómo y dónde esté apoyada la
viga. En el caso presente, el Momento flector (M), es igual a la suma
algebraica de todos los momentos que actúan a un lado de la sección
considerada, tanto a la derecha como a la izquierda de la misma, como ya
veremos mas adelante.
[1] La ley de Hooke establece que en un material elástico
sometido a una única fuerza en una dirección, la deformación relativa (e) en dicha dirección es proporcional a la tensión aplicada
(s) resultante de dicha fuerza: s = E . e
[2] Es una medida de la tendencia que tiene la fuerza aplicada
de aplastar el miembro que lo soporta, y se calcula como (MOTT, 1999):
Esfuerzo de apoyo = Fuerza aplicada /
Área de apoyo
s b = F / Ab
[3] El coeficiente de Poison corresponde a la relación entre la deformación lateral y la deformación axial de un elemento.